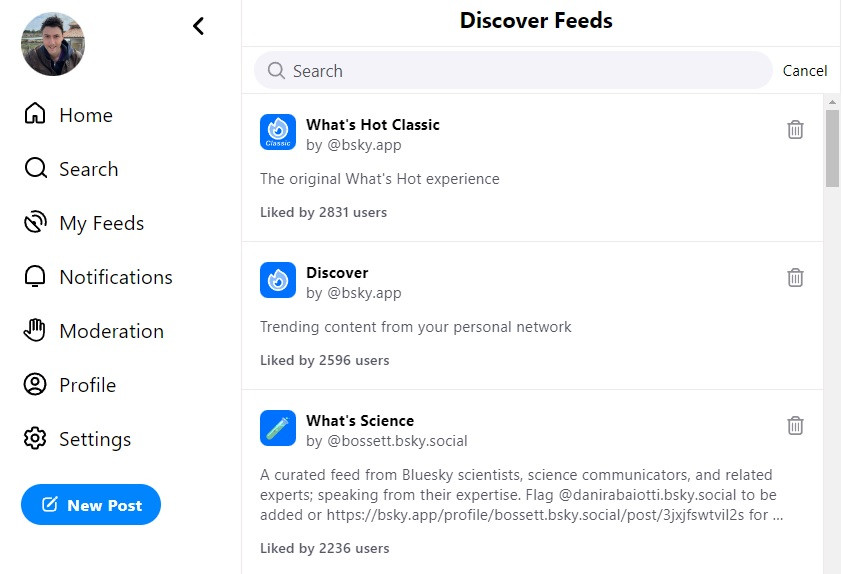
BlueSky émerge. Si vous n'êtes pas encore familier avec BlueSky, imaginez un espace en ligne qui rappelle les fonctionnalités de Twitter, où les "skeets" – équivalents des tweets – prennent vie et se propagent. Dans cet univers numérique en constante évolution, je vous propose de découvrir comment façonner votre propre expérience BlueSky. Imaginez pouvoir filtrer, trier et présenter les contenus qui résonnent le plus avec vous. C'est là qu'entre en scène le concept de "feed custom". Plutôt que d'être submergé par une avalanche d'informations, vous avez l'opportunité de choisir ce qui trouve sa place sur votre timeline. Le feed custom, c'est une carte blanche pour ajuster l'algorithme de présentation des skeets en fonction de VOS goûts et de VOS [...]

Une petite "web-app" développée sur un week-end, lors de l'ouverture de l'API ChatGPT : ApplAI.fr Rien de bien compliqué : l'objectif était de développer l'application le plus rapidement possible. Front-end : template gratuit modifié pour l'occasion (HTML & Javascript, avec bootstrap que je découvrai pour l'occasion). Back-end habituel (PHP, et API Rest Tectalic). Page d'accueil de ApplAI. [...]

Un nouveau dépôt GIT a été mis en ligne sur mon github (1) afin de mettre en ligne et de garder une trace des travaux pratiques réalisés pendant mon année au MVA de l'ENS Cachan. Ce dépôt sert à compiler les travaux pratiques du cours de vision 3D artificielle (2) donné par Monsieur Renaud Marlet (3) et par Monsieur Pascal Monasse (4). Il regroupe cinq travaux pratiques. Le premier consiste à faire de la reconstruction de panoramas. Avec deux images prises sous certaines conditions (l'appareil ayant très peu bougé notamment), on peut faire l'hypothèse que la transformation entre les deux images est restreinte à un petit [...]

Dans ce billet, je souhaite décrire mon intuition de ce qui est appelé "formulation faible", ce qui me permettra par la suite d'aborder le sujet des éléments finis dans le cadre de la résolution numérique d'équation différentielles. Volontairement, je vais choisir des exemples très concrets afin de décrire le concept. D'autre part, je préviens d'emblée qu'il y aura des abus de notation qui pourront irriter. On définit le domaine $\Omega = [0,1]\times[0,1]$. Soit $u : \Omega \rightarrow \mathbb{R}$. Soit une seconde fonction $f : \Omega \rightarrow \mathbb{R}$. On cherche à comparer les deux fonctions, et en particulier à savoir si elles sont égales. Si les deux fonctions sont égales, on peut écrire (c'est la formulation forte) : $$u(x,y) = f(x,y) \quad [...]

Aux commandes des vaisseaux spatiaux de "Elite: Dangerous", le joueur est libre de participer à tout une série d'activités. Du commerce à l'attaque pirate de vaisseaux pacifiques, de l'exploration à la conduite libre d'un vaisseau. HUD d'un vaisseau de Elite: Dangerous Pour rendre le jeu immersif, les développeurs ont rendu le pilotage de vaisseau extrèmement complexe. En plus du pilotage d'un vaisseau en trois dimension, il est par exemple possible de retirer toute les aides au pilotage stabilisant le vaisseau et il existe un nombre important d'options activables. J'ai commencé à jouer à ce jeu au clavier. Malheureusement, on [...]